gfg potd solution python 8 May 2024 | root to leaf paths gfg todays problem

Today problem of the day on geeks for geeks potd is Root to Leaf Paths on gfg 8 May 2024. This problem is an medium level questions on tree data structures. It is one of the widely asked questions by some of dream companies like Amazon and Paytm and other highly anticipated tech giants and top IT firms.

Please do not directly look for the solution for todays geeks for geeks problem of the day, instead try to learn the basic concepts about binary trees and try to define an approach that you would take to solve root to leaf paths problem using python or your favorite programming language. Have look into solution for root to leaf paths only if you are stuck.

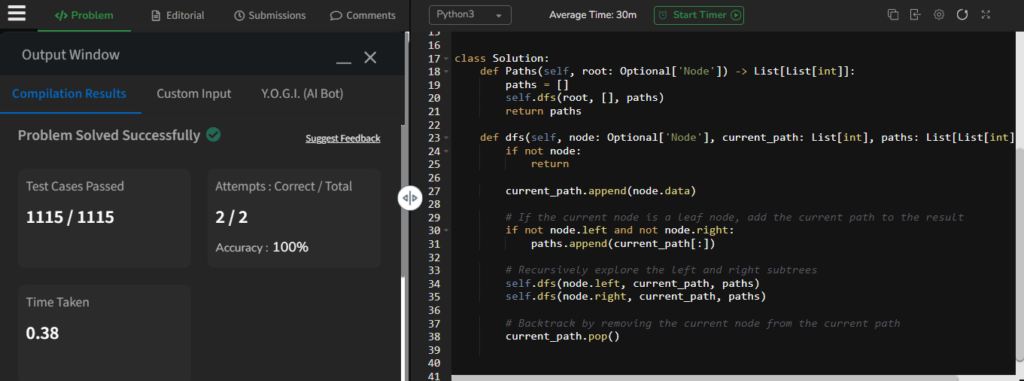
gfg potd today solution in Python

To find all possible paths from the root node to all leaf nodes (the ending nodes in a tree structure which further has no child nodes) in a binary tree, we can use a depth-first search (DFS) approach with backtracking. Let’s have the Python code to implement the Paths function:

from typing import Optional, List

class Solution:
    def Paths(self, root: Optional['Node']) -> List[List[int]]:
        paths = []
        self.dfs(root, [], paths)
        return paths

    def dfs(self, node: Optional['Node'], current_path: List[int], paths: List[List[int]]) -> None:
        if not node:
            return

        current_path.append(node.data)

        # If the current node is a leaf node, add the current path to the result
        if not node.left and not node.right:
            paths.append(current_path[:])

        # Recursively explore the left and right subtrees
        self.dfs(node.left, current_path, paths)
        self.dfs(node.right, current_path, paths)

        # Backtrack by removing the current node from the current path
        current_path.pop()

Let’s try to understand how it works!

1. The Paths function initializes an empty list paths to store all the paths from the root to leaf nodes.
2. It calls the helper function dfs with the root node, an empty current_path list, and the paths list.
3. The dfs function recursively explores the binary tree, starting from the given node.
4. If the node is None, it returns, as there is no path to explore.
5. Otherwise, it appends the node.data to the current_path list.
6. If the current node is a leaf node (i.e., it has no left or right child), it means we have found a complete path from the root to a leaf node. We append a copy of the current_path to the paths list.
7. If the current node is not a leaf node, we recursively call the dfs function for the left and right subtrees, passing the current_path and paths lists.
8. After exploring the left and right subtrees, we backtrack by removing the last element from the current_path list using current_path.pop().

The time complexity of this solution is O(n), where n is the number of nodes in the binary tree, as we visit each node once. The auxiliary space complexity is O(height of the tree) due to the recursive calls on the call stack, plus O(n) for storing the paths in the paths list.